This is going to be wild!
Question 1:
Part A:
Design a combinational circuit that counts the Numbers of 1’s in 7-bit ($I_0$ $I_1$, … $I_6$.) input and has 3-bit output. ($O_0$, $O_1$, $O_3$). And write the input equations.
Show Answer
Execuse the messy wiring!
$$O_0 = I_0 \oplus I_1 \oplus I_2 … \oplus I_7 $$ $$O_1 = $$ left as an exercise to the reader $$O_3 = $$ left as an exercise to the reader
Part B:
Design a 5-bit comparator that takes 2’s compelemnt. you can use comparators, adders, decoders, etc.
Question 2:
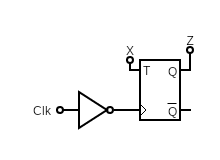
Part A:
What is the function of this circuit?
Show Answer
Toggles every negative edge as long as X is 1
Part B:
Reduce the state table (from the book)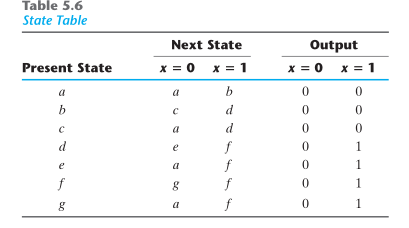
Part C:
Draw the reduced state diagram of the table
Part D:
Implement it using T-Flip Flops
Show Answer
This is left as an exercise to the reader.
Question 3:
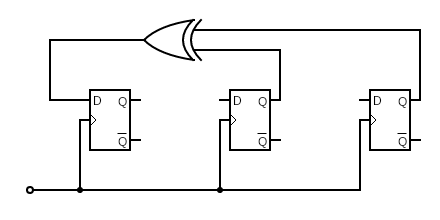
Part A:
Given the current state is ABC = 100. What is the state for the next 7 cycles?
Show Answer
$$ A(t+1) = B \oplus C $$ $$ B(t+1) = A $$ $$ C(t+1) = C $$ $$ ABC(0) = 100 $$ $$ ABC(1) = 010 $$ $$ ABC(2) = 101 $$ $$ ABC(3) = 110 $$ $$ ABC(4) = 111 $$ $$ ABC(5) = 011 $$ $$ ABC(6) = 001 $$ $$ ABC(7) = 100 $$
Part B:
Convert the following D-FF serial adder to a T-FF: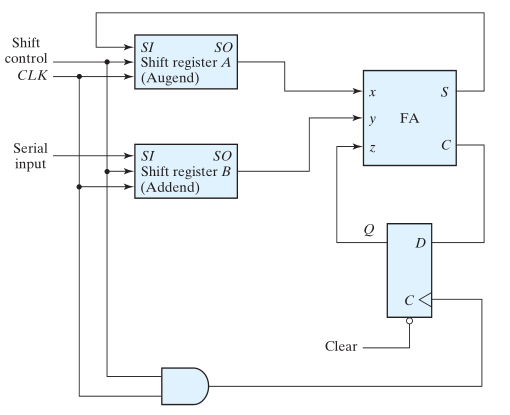
Show Answer
Easy Solution: Convert the T-FlipFlop back to a D-FlipFlop! (i.e,
implement a D-FlipFlop with a T-Flipflop)
Standard Solution: do the truth table, K-maps, equations, etc.
This is left as an exercise to the reader.
Part C:
Given that all the registers are set to 1011, what is the value of
register A after: 4, 8, 12 and 16 cycles. Initially, the Flip was
set to 0, (or Reset).
Also, Register B is always filled with 1011 every 4 cycles! I am just too lazy to
draw that :)
Show Answer
We can see that after 4 cycles, $A(t+4)=A + B + C $
We can also see the $C=$ carry of A’s sum
Initially
$$ A (0) = 0 $$
$$ C (0) = 0 $$
After 4 cycles:
$$ A (4) = 1011 + 1011 + 0 = 0110 $$
$$ C (4) = 1$$
After 8 cycles: $$ A (8) = 0110 + 1011 + 1 = 0010 $$ $$ C (8) = 1$$
After 12 cycles: $$ A (12) = 0010 + 1011 + 1 = 0010 $$ $$ C (12) = 1$$
After 16 cycles: $$ A (16) = 0110 + 1011 + 1 = 1110 $$ $$ C (16) = 0$$
Part D:
Given the following truth table,
| x | y | z | A | B | C | D |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| 1 | 0 | 1 | 1 | 1 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 | 1 | 0 |
| 1 | 1 | 1 | 0 | 0 | 0 | 1 |
implement it using the following PAL after filling the table.
Show Equations
Do the K-maps, then you get:
$$ A = \bar{z} + x \oplus y $$
$$ B = \overline{x \oplus y \oplus z} $$
$$ C = x \oplus z$$
$$ D = z + x \oplus y $$
Show Simplified Equations
$B$ can be simplifed as $$ B = \overline{y \oplus C } $$ Which can be furthur simplified as $$ B = \bar{y} \oplus C $$
Also if you are wondering how tf $\oplus$ and $\bar{\oplus}$ are implemented using AND and OR gates, refer to the book.
Show Table
This is left as exercise to the reader.